Skip to contents

Chapter 6: The Bayesian Approach to Standard Regression Analysis

Chapter06.Rmd

Section 6.2 Bayesian Learning for a Standard Linear Regression Model

Example 6.1: Movie data

We use movie data provided within the package to illustrate Bayesian analysis of a regression model. The data set is a preprocessed version of the one provided by Lehrer and Xi (2017).

library("BayesianLearningCode")
data("movies", package = "BayesianLearningCode")

Section 6.2.1 Bayesian Learning Under Improper Priors

Example 6.2: Movie data

We define the response variable OpenBoxOffice, which contains the box office sales at the opening weekend in Mio.$ as y and use the budget (Budget, in Mio.$) and the predetermined number of screens (Screens, in 1000) the film was forecast to be in theaters six weeks prior to opening as covariates.

We center the covariates budget and screens at their means in the data set. Thus the intercept is the sales on the opening weekend box office (in Mio. $) of a film with average budget and forecast to be in the theaters on the average number of screens .

y <- movies[, "OpenBoxOffice"]
covs <- c("Budget", "Screens")
covs.cen <- scale(movies[, covs], scale = FALSE) # center the covariates

N <- length(y)  # number of observations

X <- as.matrix(cbind("Intercept" = rep(1, N), covs.cen)) # regressor matrix
d <- dim(X)[2] # number regression effects

We then define a function to compute the parameters of the posterior distribution of the regression effects under the improper prior p(β,σ2)∝1σ2p(\beta, \sigma^2) \propto \frac{1}{\sigma^2}.

regression_improper <- function(y, X) {
  
   BN <- solve(crossprod(X))
   Xy <- crossprod(X, y)
   beta.hat <- BN %*% Xy

   SSR <- as.numeric(crossprod(y - X %*% beta.hat))

   cN <- (N - d) / 2
   CN <- SSR / 2

   post.var <- (CN / cN) * BN
   list(beta.hat = beta.hat, BN = BN, cN = cN, CN = CN, post.var=post.var)
}

The following table reports the posterior means together with their equal-tailed 95% credibility intervals.

reg.improp <- regression_improper(y,X)

beta.hat <- reg.improp$beta.hat
post.sd = sqrt(diag(reg.improp$post.var))
cN<- reg.improp$cN

knitr::kable(round(cbind(qt(0.025,df = 2 * cN) * post.sd + beta.hat,
                          beta.hat,
                         qt(0.975,df = 2 * cN) * post.sd + beta.hat), 3),
             col.names = c("2.5% quantile", "posterior mean", "97.5% quantile"))
2.5% quantile posterior mean 97.5% quantile
Intercept 15.977 19.110 22.243
Budget 0.009 0.174 0.339
Screens 1.073 1.719 2.365

The expected sales on the opening weekend box office is 19.11 Mio.$ for a film with an average and forecast to be shown on an average number of . For such a film the expected box office sales on the opening weekend are 0.174 Mio.$ higher if the budget is 1 Mio.$ higher; for a film to be shown on 1000 screens more with an average budget the expected box office sales are 1.719 Mio.$ higher.

To show the uncertainty of the estimates, we plot the (univariate) marginal posterior distribution of the intercept as well as the univariate and bivariate marginal posterior distributions of the covariate effects.

par(mar = c(3, 2, 1, 1))
curve(dt((x - beta.hat[1]) / post.sd[1], df = 2 *cN),
      from = beta.hat[1] - lim[1],
      to = beta.hat[1] + lim[1],
      ylab = "", xlab = "", main = "")
mtext("Intercept", 1, line = 1.7)

f <- function(x1, x2) {
  mvtnorm::dmvt(cbind(x1 - beta.hat[2], x2 - beta.hat[3]),
                sigma = reg.improp$post.var[2:3, 2:3], df = 2 * reg.improp$cN, log = FALSE)
}

xx1 <- seq(-lim[2], lim[2], length = 201) + beta.hat[2]
xx2 <- seq(-lim[3], lim[3], length = 201) + beta.hat[3]
z <- outer(xx1, xx2, f)

par(mar = c(3, 3, 1, 1))
contour(xx1, xx2, z, add = FALSE)
mtext(rownames(beta.hat)[2], 1, line = 1.7)
mtext(rownames(beta.hat)[3], 2, line = 1.7)

par(mar = c(0, 3, 1, 1))
mar.x1 <- dt((xx1 - beta.hat[2]) / post.sd[2], df = 2 * reg.improp$cN,
             log = FALSE)
plot(xx1, mar.x1,  type = "l", xaxt = "n", ylab = "")

par(mar = c(3, 0, 1, 1))
mar.x2 <- dt((xx2 - beta.hat[3]) / post.sd[3], df = 2 * reg.improp$cN,
             log = FALSE)
plot(mar.x2, xx2,  type = "l", yaxt = "n", xlab = "")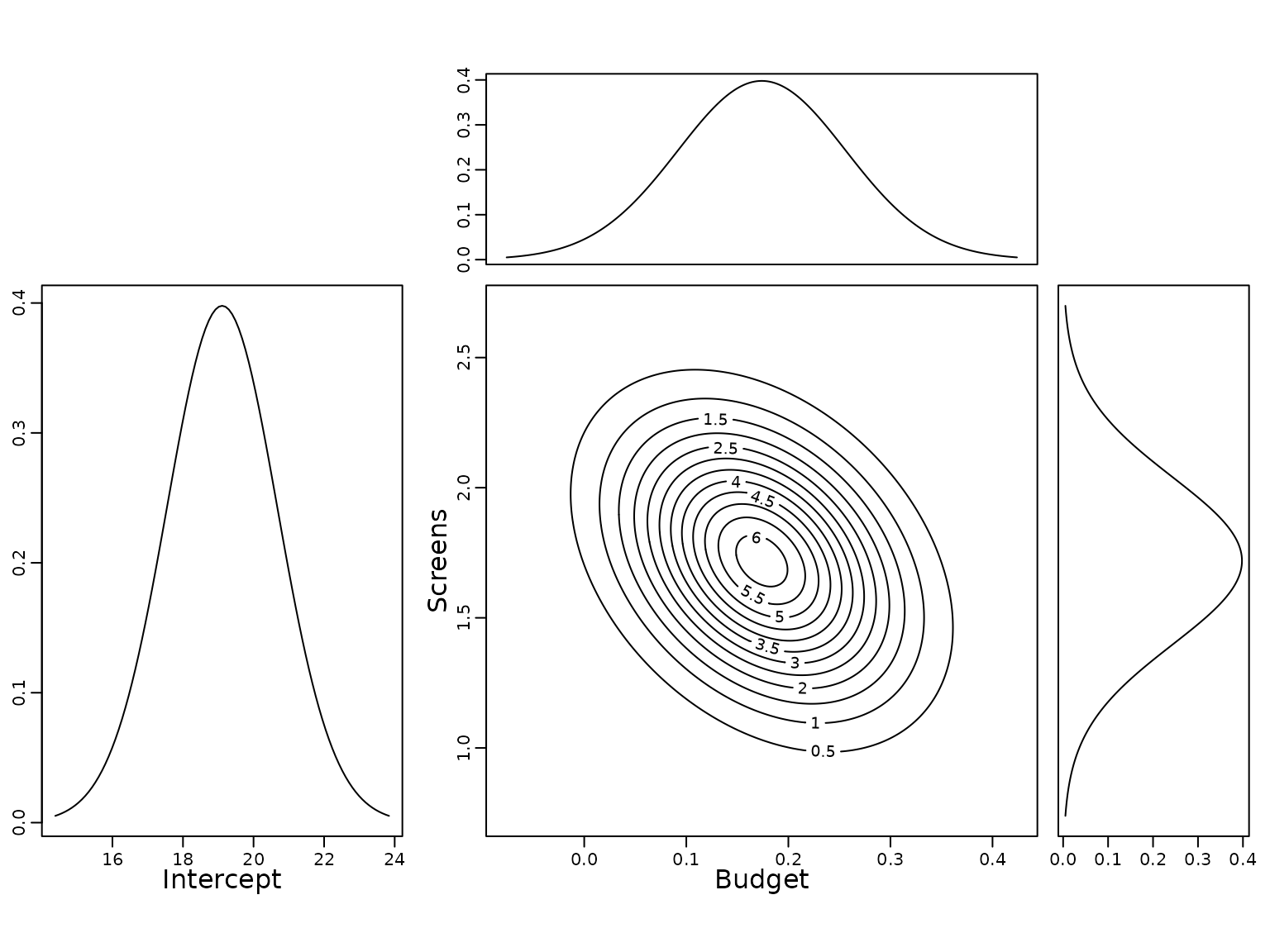

For completeness we finally report also the posterior expectation of the error variance and its 95% credibility interval.

sigma2.hat <- reg.improp$CN /(cN-1)
knitr::kable(round(cbind(qinvgamma(0.025,a=cN,b=reg.improp$CN), sigma2.hat,
                     qinvgamma(0.975,a=cN,b=reg.improp$CN)),2),
             col.names = c("2.5% quantile", "posterior mean", "97.5% quantile"))
2.5% quantile posterior mean 97.5% quantile
178.38 239.07 319.96

Exercise 6.3.

We now are interested in predicting of the box office sales on the opening weekend. We compute the predicted box office sales for a film with an average number of for a range of values for .

 xvals <-  -30:60
 nf <-length(xvals) 
 X_new <- cbind(rep(1,nf),xvals,rep(0,nf))
 colnames(X_new)<-colnames(X)
 
 ypred=X_new %*% beta.hat 
 ypred.var=rep(NA, nf)
 for (i in (1:nf)){
      ypred.var[i] <-sigma2.hat*(t(X_new[i,])%*%reg.improp$BN%*%X_new[i,]+1)
 }

The following plot shows the point predictions together with the 50% and 80% prediction intervals.

par(mar = c(3, 3, 1, 1))
budget=X_new[,2]+mean(movies[, "Budget"])
plot(budget,ypred, type="l",lwd=2,ylim=c(-20,60),
     xlab="Budget",ylab="Predicted box office sales")

pred.levels=c(0.5,0.8)
for (j in (1:length(pred.levels))){
     pred.quantile <- qt(1-(1-pred.levels[j])/2,df=2*cN)
     lines(budget, ypred - sqrt(ypred.var)*pred.quantile, lty=j+1)
     lines(budget, ypred + sqrt(ypred.var)*pred.quantile, lty=j+1)
}
legend("bottomright", c("Predicted mean",
            paste(pred.levels[1]*100,"% Prediction interval"),                                   paste(pred.levels[2]*100,"% Prediction interval"))  ,
            lty = 1:3, lwd = c(2, 1, 1))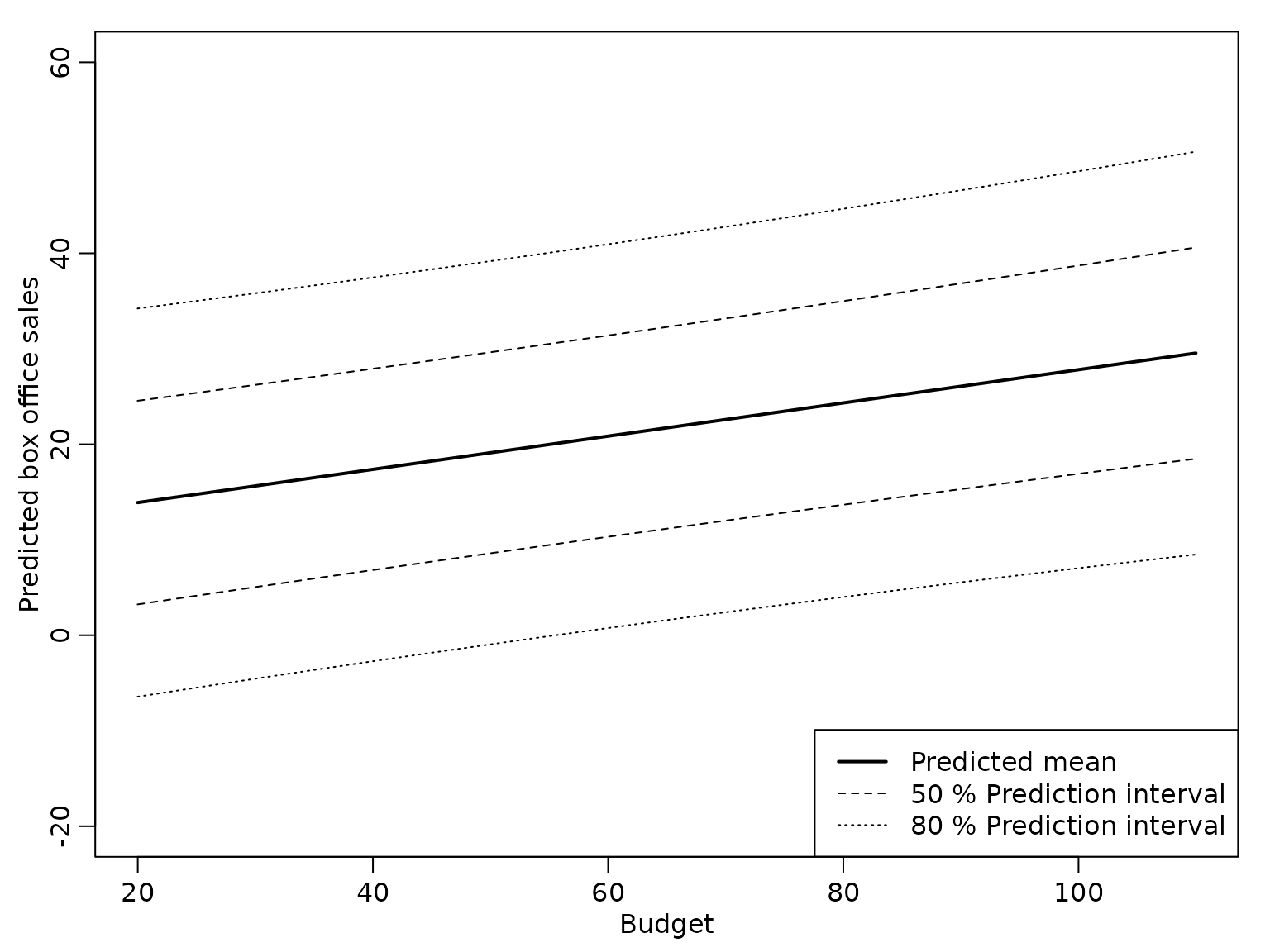

plot(y, y.pred,xlim=c(-20,160), ylim=c(-20,160), 
     xlab="observed sales", ylab="predicted sales")
abline(a=0, b=1)
abline(h=0,lty=2)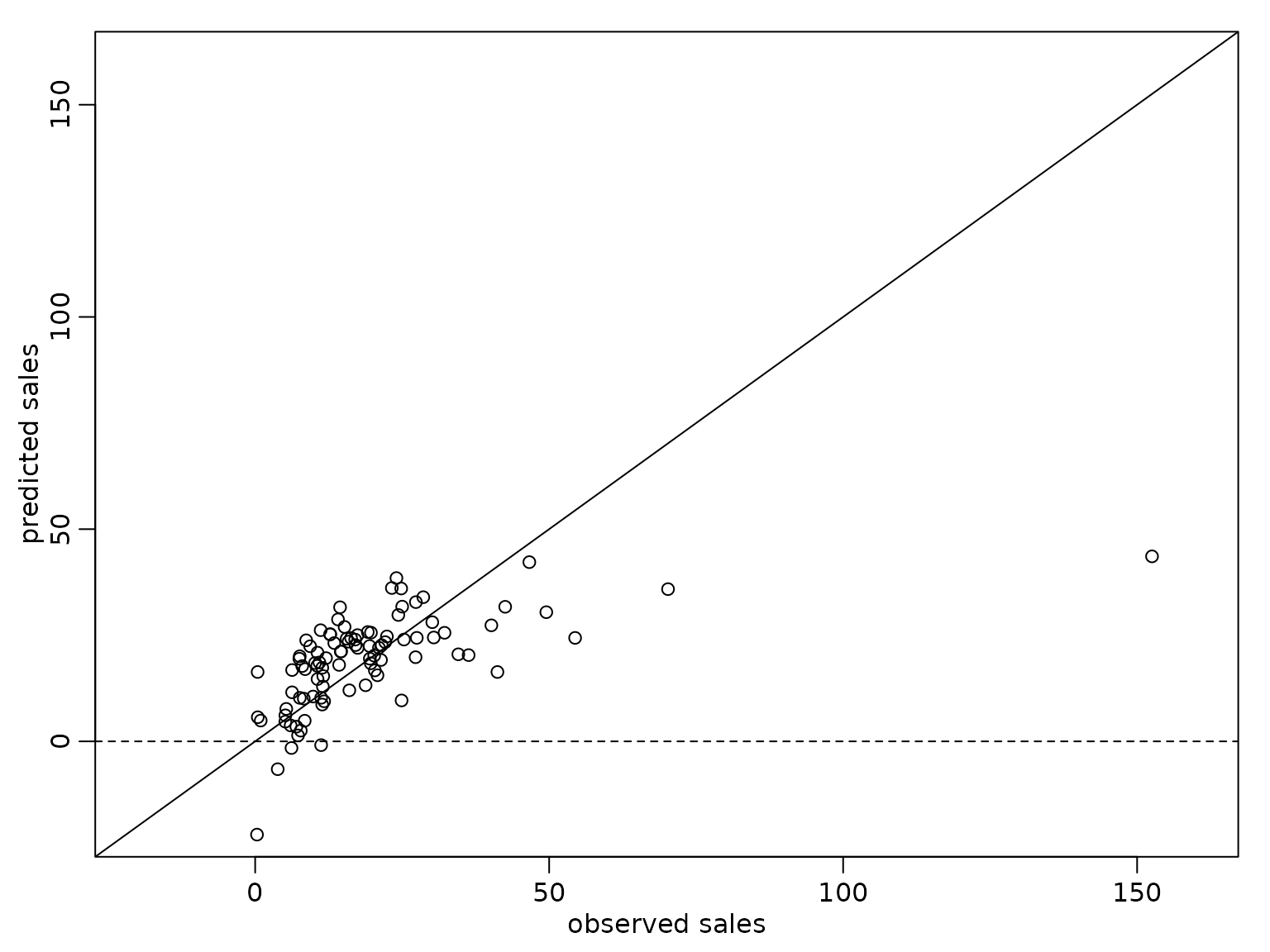

The prediction interval is symmetric around the posterior mean, but obviously the model is not adequate, as the lower limit of the 80%-prediction interval is negative for a budget below ~55 Mio.$.

We can take into account that box office sales are always positive by fitting a linear regression model on the log transformed sales.

log.y <- log(movies[, "OpenBoxOffice"])
reg.lny<- regression_improper(log.y,X)

lny.pred <- X_new %*% reg.lny$beta.hat 
sigma2.hat <- reg.lny$CN /(reg.lny$cN-1)

lny.pred.var=rep(NA, nf)
for (i in (1:nf)){
     lny.pred.var[i]<-sigma2.hat*(t(X_new[i,])%*%reg.lny$BN%*%X_new[i,]+1)
}

From the estimation results we determine the point predictions and prediction intervals for the logarithm of the box office sales and exponentiate the results to obtain the predictions for the sales.

The following figure shows the point prediction with the 50% and 80% prediction intervals for the box office sales for a film shown on an average number of for a range of values for derived from this model.

plot(budget,exp(lny.pred), type="l",ylim=c(-20,60),col="blue",
     xlab="Budget",ylab="Predicted box office sales", lwd=2)

for (j in (1:length(pred.levels))){
     pred.quantile <- qt(1-(1-pred.levels[j])/2,df=2*reg.lny$cN)
     lines(budget, exp(lny.pred - sqrt(lny.pred.var)*pred.quantile), 
           col="blue", lty=j+1)
     lines(budget, exp(lny.pred + sqrt(lny.pred.var)*pred.quantile), 
           col="blue", lty=j+1)
}
legend("bottomright", c("Predicted mean",
            paste(pred.levels[1]*100,"% Prediction interval"),                                   paste(pred.levels[2]*100,"% Prediction interval"))  ,
            col="blue",lty = 1:3, lwd = c(2, 1, 1))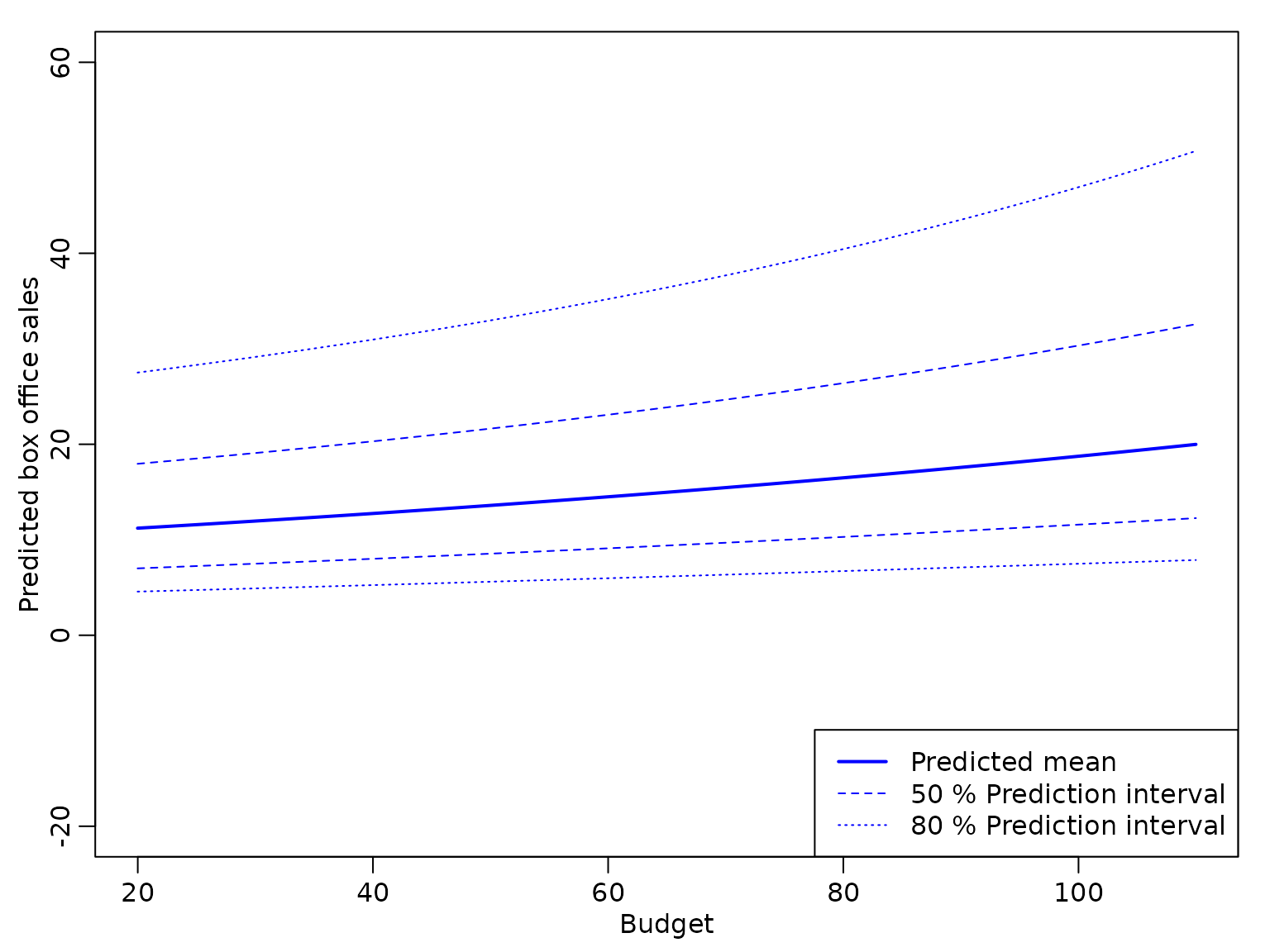

We see that the bounds of the prediction intervals are positive, but – due to the exponential transformation – the prediction intervals are no longer symmetric around the point predictions.

We next compare the point predctions from both models to the observed sales.


plot(y, y.pred,xlim=c(-20,160), ylim=c(-20,160),  xlab="Observed sales", ylab="Predicted sales")

points(y,exp(X%*%reg.lny$beta.hat),col="blue", pch=16)
abline(a=0, b=1)
abline(h=0,lty=2)
legend("bottomright", c("Linear regression on y","Linear regression on ln(y)"),
                      col=c("black","blue"),lty=1)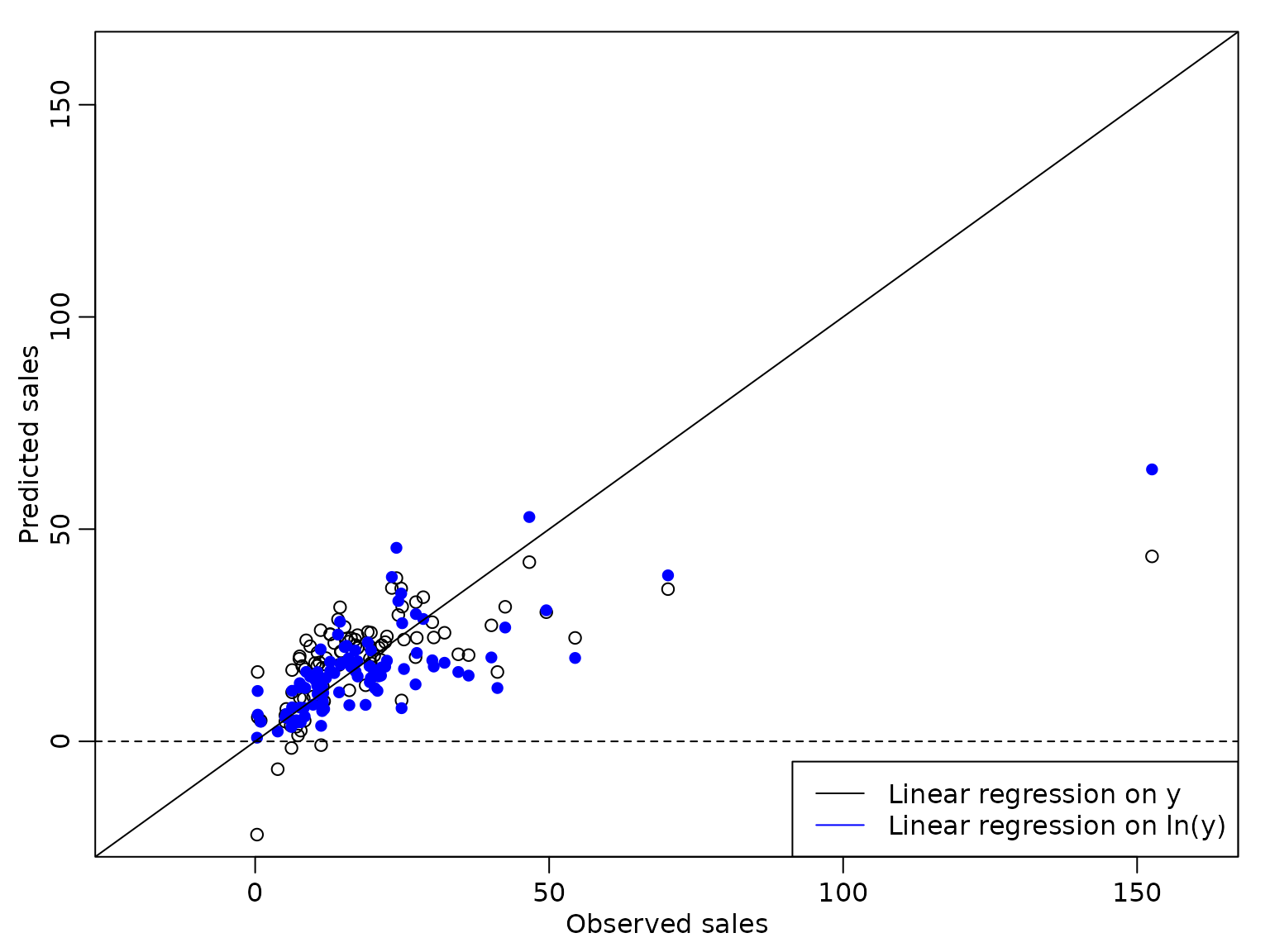

We see that those from the regression model on the logarithm of the box office sales are slightly better, but the observed box office sales of 152 Mio.$ are still predicted much too low.

Section 6.2.2 Bayesian Learning under Conjugate Priors

We next consider regression analysis under a conjugate prior. For this, we first define a function that yields the parameters of the posterior distribution.

regression_conjugate <- function(y, X, b0 = 0, B0 = 10, c0 = 0.01, C0 = 0.01) {
  d <- ncol(X)
  if (length(b0) == 1L)
    b0 <- rep(b0, d)
  
  if (!is.matrix(B0)) {
    if (length(B0) == 1L) {
      B0 <- diag(rep(B0, d))
    } else {
      B0 <- diag(B0)
    }
  }
  
  B0.inv <- solve(B0)
  BN.inv <- B0.inv + crossprod(X)
  
  BN <- solve(BN.inv)
  bN <- BN %*% (B0.inv %*% b0 + crossprod(X, y))
  
  cN <- c0 + N / 2
  SS.eps <- as.numeric(crossprod(y) + t(b0) %*% B0.inv %*% b0 -
                         t(bN) %*% BN.inv %*% bN)
  CN <- C0 + SS.eps / 2
  list(bN = bN, BN = BN, cN = cN, CN = CN)
}

We specify a Normal prior with mean zero and 𝐁0=λ2𝐈\mathbf{B}_0=\lambda^2 \mathbf{I} with λ2=10\lambda ^2=10 on the regression effects and an inverse Gamma prior with c0=2.5c_0=2.5 and C0=1.5C_0=1.5 on σ2\sigma^2. With this choice of the prior parameters c0c0 and C0C_0 the prior is rather uninformative but guarantees existence of the posterior variance.

We perform a regression analysis on the box office sales yy and report the posterior mean of the regression effects together with the 2.5% and 97.5% quantile of the posterior distribution in the following table.

res_conj1 <- regression_conjugate(y, X, b0 = 0, B0 = 10, c0=2.5, C0=1.5)
post.sd.conj1 = sqrt(diag((res_conj1$CN / res_conj1$cN) * res_conj1$BN))

knitr::kable(round(cbind(
    qt(0.025, df = 2 * res_conj1$cN) * post.sd.conj1 + res_conj1$bN,
    res_conj1$bN,
    qt(0.975, df = 2 * res_conj1$cN) * post.sd.conj1 + res_conj1$bN), 3), 
    col.names = c("2.5 quantile", "posterior mean", "97.5 quantile"))
2.5 quantile posterior mean 97.5 quantile
Intercept 16.088 19.090 22.091
Budget 0.016 0.174 0.332
Screens 1.099 1.719 2.339

To illustrate the effects of a tighter prior on the regression effects we next compute the posterior parameters also for λ2=1\lambda^2=1 and λ2=0.1\lambda^2=0.1.

res_conj2 <- regression_conjugate(y, X, b0 = 0, B0 = 1, c0=2.5, C0=1.5)
post.sd.conj2 = sqrt(diag((res_conj2$CN / res_conj2$cN) * res_conj2$BN))

res_conj3<- regression_conjugate(y, X, b0 = 0, B0 = 0.1, c0=2.5, C0=1.5)
post.sd.conj3 = sqrt(diag((res_conj3$CN / res_conj3$cN) * res_conj3$BN))

We plot the marginal posteriors together with those under the improper prior.

for (i in seq_len(nrow(beta.hat))) {
  curve(dt((x - beta.hat[i]) / post.sd[i], df = 2 * cN),
    from = beta.hat[i] - 4 * post.sd[i], 
    to  =  beta.hat[i] + 4 * post.sd[i],
    ylab = "", xlab = "" , main = rownames(beta.hat)[i])
  
  curve(dt((x - res_conj1$bN[i]) / post.sd.conj1[i], 
          df = 2 * res_conj1$cN),
    from = res_conj1$bN[i] - 4 * post.sd.conj1[i],
    to  =  res_conj1$bN[i] + 4 * post.sd.conj1[i],
    add = TRUE, col = 2, lty = 2, lwd = 2)
  
  curve(dt((x - res_conj2$bN[i]) / post.sd.conj2[i], 
           df = 2 * res_conj2$cN),
    from = res_conj2$bN[i] - 4 * post.sd.conj2[i],
    to  =  res_conj2$bN[i] + 4 * post.sd.conj2[i], 
    add = TRUE, col = 3,lty = 3, lwd = 2)
  
  curve(dt((x - res_conj3$bN[i]) / post.sd.conj3[i], 
           df = 2 * res_conj3$cN),
    from = res_conj3$bN[i] - 4 * post.sd.conj3[i],
    to  =  res_conj3$bN[i] + 4 * post.sd.conj3[i],
    add = TRUE, col = 4,lty = 4, lwd = 2)
  
  legend("topright", c("improper", 
                       expression(paste(lambda^2,"=", 10)), 
                       expression(paste(lambda^2, "=", 1)),
                       expression(paste(lambda^2,"=", 0.1))),
    col = 1:4, lty = 1:4, lwd = c(1, 2, 2, 2))
}

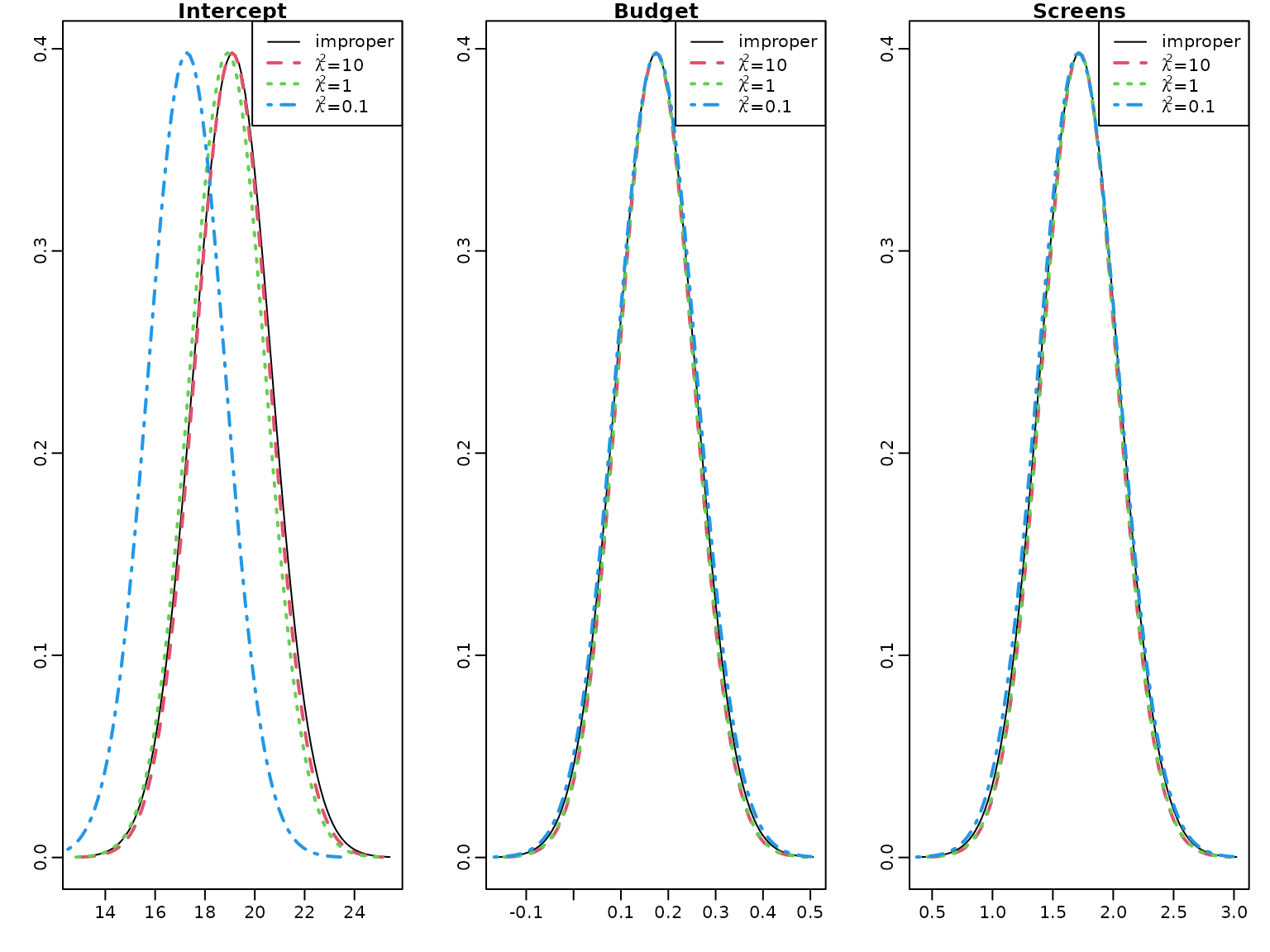
There is little difference to the improper prior for the effects of Budget and Screens, however the intercept intercept is shrunk to zero for λ2=1\lambda^2=1 and even more for λ2=0.1\lambda^2=0.1.

To illustrate the effect of the prior we compute the the weight matrix 𝐖\textbf{W} for the conjugate prior with mean 𝟎\textbf{0} and covariance matrix λ2𝐈\lambda^2 \textbf{I} for λ2=0.1\lambda^2=0.1.

W <- res_conj3$BN %*% solve(diag(rep(0.1, d)))
print(round(W, 3),digits=3)
#>            [,1] [,2]  [,3]
#> Intercept 0.096    0 0.000
#> Budget    0.000    0 0.000
#> Screens   0.000    0 0.005

Obviously the weight of the prior mean is much larger for the intercept than for the effects of the Weeks and Screens. Together with the high value of the posterior mean of the intercept this explains the considerable shrinkage to zero of the intercept, whereas the effects of the two covariates are almost unshrunk.

6.3 Regression Analysis under the Semi-Conjugate Prior

We now include all available covariates in the regression analysis. As there is only one film with MPAA rating G'', we merge the two ratingsG’’ and ``PG’’ into one category which we define as our baseline.

movies["PG"] <- NULL

Next, we center all covariates at zero and define the regressor matrix.

covs <- c("Comedy", "Thriller","PG13", "R", "Budget", "Weeks", "Screens", 
          "S-4-6", "S-1-3", "Vol-4-6", "Vol-1-3")
covs.cen <- scale(movies[, covs], scale = FALSE)

N <- length(y)  # number of observations
X <- cbind("Intercept" = rep(1, N), covs.cen) # regressor matrix

d <- dim(X)[2] # number regression effects 
p <- d - 1 # number of regression effects without intercept

To estimate the parameters of the regression model under a rather flat semi-conjugate prior, we first set up the Gibbs sampler.

set.seed(1)

reg_semiconj <- function(y, X, b0 = 0, B0 = 10000, c0 = 2.5, C0 = 1.5,
                   burnin = 1000L, M = M) {
    d <- dim(X)[2] 
    B0inv <- diag(rep(1 / B0, d), nrow = d)
    b0 <-  rep(b0, length.out = d)

    # define quantities for the Gibbs sampler
    XX <- crossprod(X)
    Xy <- t(X) %*% y
    cN <- c0 + N / 2
    
    # prepare storing of results
   betas <- matrix(NA_real_, nrow = M, ncol = d)
   colnames(betas) <- colnames(X)

   sigma2s <- rep(NA_real_,  M)

   # starting value for sigma2
   sigma2 <- var(y) / 2

   for (m in 1:(burnin + M)) {
       # sample beta from the full conditional
       BN <- solve(B0inv + XX / sigma2) 
       bN <- BN %*% (B0inv %*% b0 + Xy / sigma2)
       beta <- t(mvtnorm::rmvnorm(1, mean = bN, sigma = BN))
    
       # sample sigma^2 from its full conditional
       eps <- y - X %*% beta
       CN <- C0 + crossprod(eps) / 2
       sigma2 <- rinvgamma(1, cN, CN)
      
       if (m > burnin) {
          betas[m - burnin, ] <- beta
          sigma2s[m - burnin] <- sigma2
       }
   }
   return(post.draws = list(betas = betas, sigma2s = sigma2s))
}

Next, we define the prior parameters and run the sampler.

M <- 20000L # number of draws after burn-in
post.draws <- reg_semiconj(y, X, b0 = 0, B0 = 10000, c0 = 2.5, C0 = 1.5,
                   burnin = 1000L, M = M)

To summarize the results nicely, we compute equal-tailed 95% confidence intervals for the regression effects.

res.mcmc <- function(x, lower = 0.025, upper = 0.975)
  c(quantile(x, lower), mean(x), quantile(x, upper))

beta.sc <- post.draws$betas

res_beta.sc<- t(apply(beta.sc, 2, res.mcmc))
colnames(res_beta.sc) <- c("2.5%", "Mean", "97.5%") 
rownames(res_beta.sc) <- c("Intercept", covs)

knitr::kable(round(res_beta.sc, 3))
2.5% Mean 97.5%
Intercept 17.501 19.104 20.714
Comedy -2.730 1.453 5.544
Thriller -3.972 0.535 4.967
PG13 -8.441 -2.741 3.000
R -3.634 2.197 8.038
Budget 0.040 0.128 0.215
Weeks 0.022 0.380 0.742
Screens 0.596 0.964 1.332
S-4-6 -4.835 -1.274 2.350
S-1-3 -1.202 2.449 6.117
Vol-4-6 -19.648 -16.726 -13.766
Vol-1-3 19.283 22.365 25.458

We do the same for the error variances.

sigma2.sc<-post.draws$sigma2s
res_sigma2.sc <- res.mcmc(sigma2.sc)
names(res_sigma2.sc) <- colnames(res_beta.sc)
knitr::kable(t(round(res_sigma2.sc, 3)))
2.5% Mean 97.5%
47.415 63.815 86.276

6.4 Regression Analysis Based on the Horseshoe Prior

A comparison of the normal and the horseshoe prior shows that the latter has much more mass close to zero and fatter tails.

beta <- seq(from = -4, to = 4, by = 0.01)

# Horseshoe prior
# Approximated by the result of Theorem 1 in Carvalho and Polson (2010)
c <-  1 / sqrt(2 * pi^3)
l <- c / 2 * log(1 + 4 / beta^2)
u <- c * log(1 + 2 / beta^2)
par(mfrow = c(1, 1))
plot(beta, (u + l) / 2, type = "l", ylim = c(0, 0.55), xlab = expression(beta),
     ylab = "", lty = 1, col = "blue")
lines(beta, dnorm(beta), lty = 2) # Standard normal prior
legend('topright', legend = c("Horseshoe", "Standard normal"), lty = 1:2,
       col = c("blue", "black"))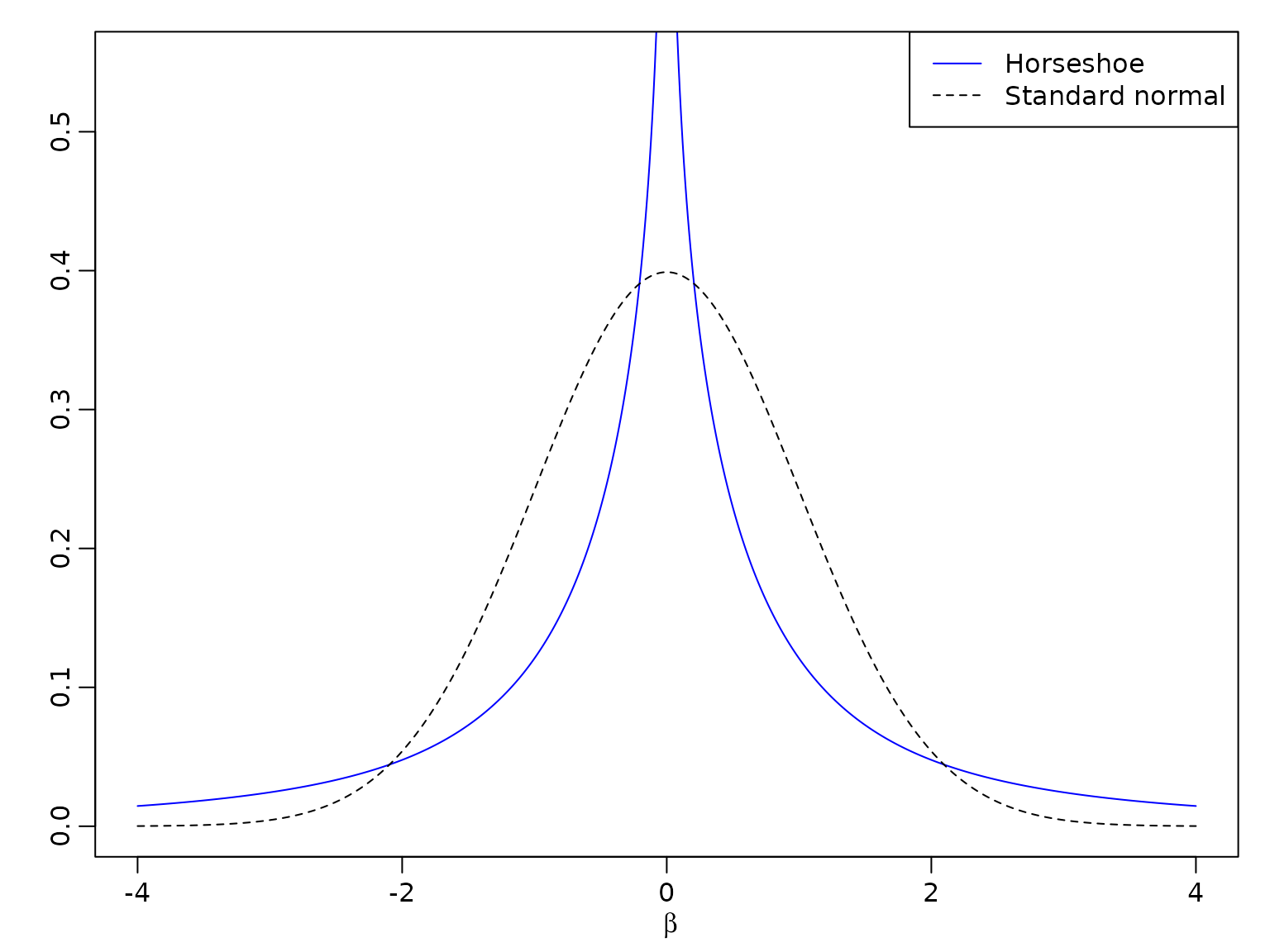

We now set up the Gibbs sampler of the regression model wIth a proper Normal prior on the intercept and horseshoe priors on the covariate effects.

reg_hs <- function(y, X,  b0 = 0, B0 = 10000, c0 = 2.5, C0 = 1.5,
                   burnin = 1000L, M) {
   d <- dim(X)[2]
   p <- d - 1
   
   B00inv <- 1 / B0 # prior precision for the intercept
   b0 <-  rep(b0, length.out = d)

   # prepare storing of results
   betas <- matrix(NA_real_, nrow = M, ncol = d)
   colnames(betas) <- colnames(X)
   
   sigma2s<- rep(NA_real_, M)
   tau2s <- matrix(NA_real_, nrow =  M, ncol = p)
   lambda2s <- rep(NA_real_,  M)
   
   # define quantities for the Gibbs sampler
   XX <- crossprod(X)
   Xy <- crossprod(X, y)

   # set starting values 
   sigma2 <- var(y) / 2
   tau2 <- rep(1, p)
   lambda2 <- 1

   for (m in seq_len(burnin + M)) {
       # sample  beta from the full conditional
       B0inv <- diag(c(B00inv, 1 / (lambda2 * tau2)))
       BN <- solve(B0inv + XX / sigma2) 
       bN <- BN %*% (B0inv %*% b0 + Xy / sigma2)
  
       beta <- t(mvtnorm::rmvnorm(1, mean = bN, sigma = BN))
       beta.star <- beta[2:d]
  
       # sample sigma^2 from its full conditional
       eps <- y - X %*% beta
       CN <- C0 + crossprod(eps) / 2
       sigma2 <- rinvgamma(1, cN, CN)
  
      # sample tau^2
      xi  <- rexp(p, rate = 1 + 1 / tau2)
      tau2 <- rinvgamma(p, 1, xi + 0.5 * beta.star^2 / lambda2)
  
      # sample lambda^2
      zeta <- rexp(1, rate = 1 + 1 / lambda2)
      lambda2 <- rinvgamma(1, (p + 1) / 2, zeta + 0.5 * sum(beta.star^2 / tau2))
  
      # store results
      if (m > burnin) {
         betas[m - burnin, ] <- beta
         sigma2s[m - burnin] <- sigma2
         tau2s[m - burnin,] <- tau2
         lambda2s[m - burnin] <- lambda2
      }
   }
   list(betas = betas, sigma2s = sigma2s, tau2s = tau2s, lambda2s = lambda2s)
}

We estimate the parameters in the regression model with the same prior on intercept and error variance as in the semi-conjugate prior, but a horseshoe prior on the covariate effects.

post.draws.hs <- reg_hs(y, X, M = M)

Again, we show the posterior mean estimates of the regression effects together with their equal-tailed 95% credibility intervals in a table.

beta.hs <- post.draws.hs$betas
res_beta.hs <- t(apply(beta.hs, 2, res.mcmc))
colnames(res_beta.hs) <- c("2.5%", "Mean", "97.5%")
rownames(res_beta.hs) <- colnames(X)
knitr::kable(round(res_beta.hs, 3))
2.5% Mean 97.5%
Intercept 17.405 19.110 20.804
Comedy -1.675 0.255 2.863
Thriller -2.309 0.039 2.546
PG13 -6.504 -1.803 0.829
R -1.421 0.953 5.009
Budget 0.027 0.125 0.217
Weeks -0.012 0.334 0.701
Screens 0.576 0.959 1.344
S-4-6 -1.551 0.237 1.731
S-1-3 -0.557 0.735 2.686
Vol-4-6 -19.179 -16.094 -12.976
Vol-1-3 18.503 21.702 24.871

We also report the estimation results for the error variance.

sigma2.hs<-post.draws.hs$sigma2s

res_sigma2.hs <- res.mcmc(sigma2.hs)
names(res_sigma2.hs) <-c("2.5%", "Mean", "97.5%")

knitr::kable(t(round(res_sigma2.hs, 3)))
2.5% Mean 97.5%
51.392 70.115 95.35

Obviously, taking into account more covariates the posterior mean of the error variance is considerably lower than in the model with only Weeks and Screens used as covariates.

We next have a look at the posterior distributions. The plots on the left hand side show the posterior distribution for the regression effects under the semi-conjugate prior, those on the right hand side the posterior distributions under the horseshoe prior. Note that the posterior distributions are symmetric under the semi-conjugate prior, whereas this is not the case under the horseshoe prior.

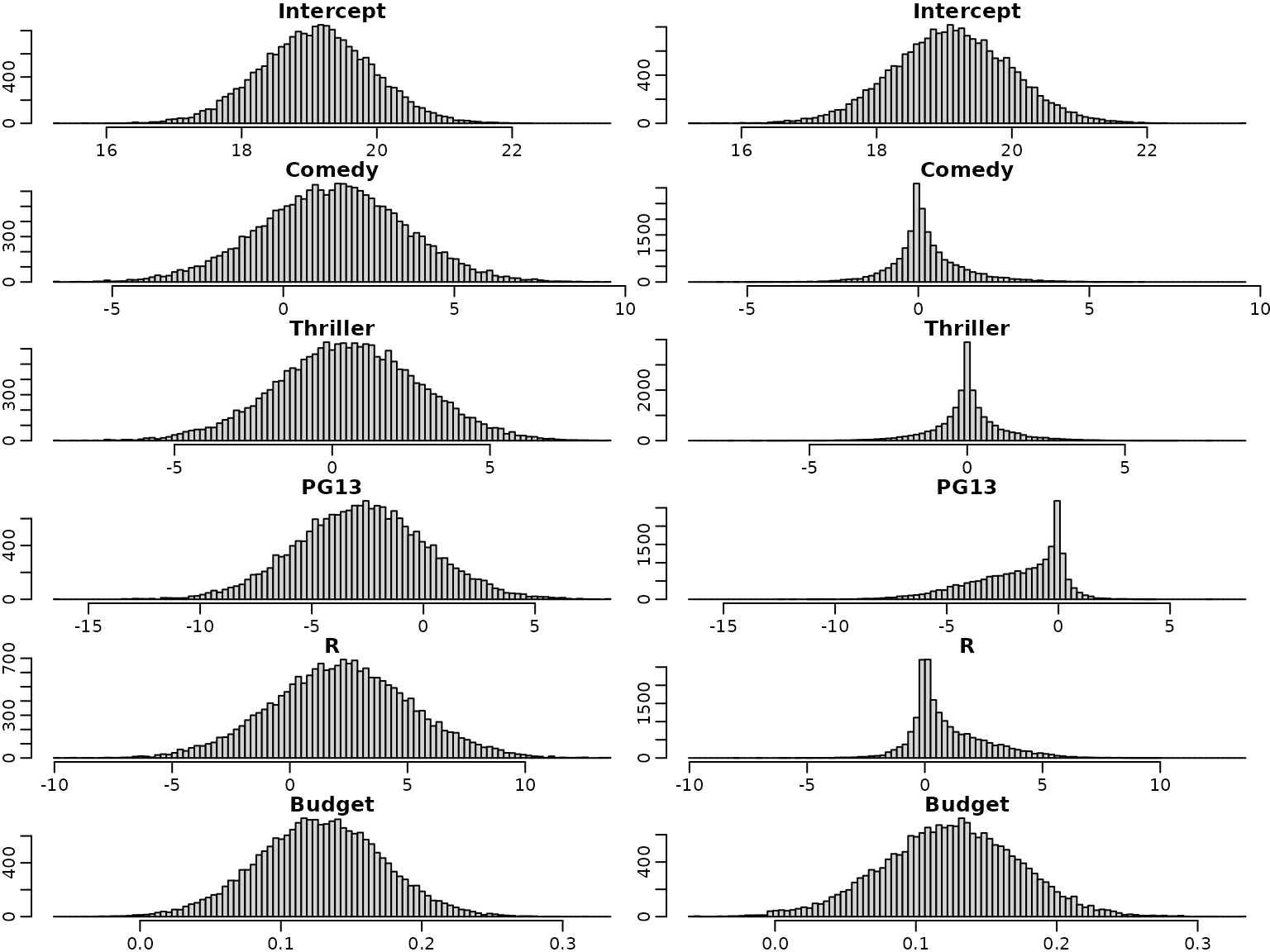
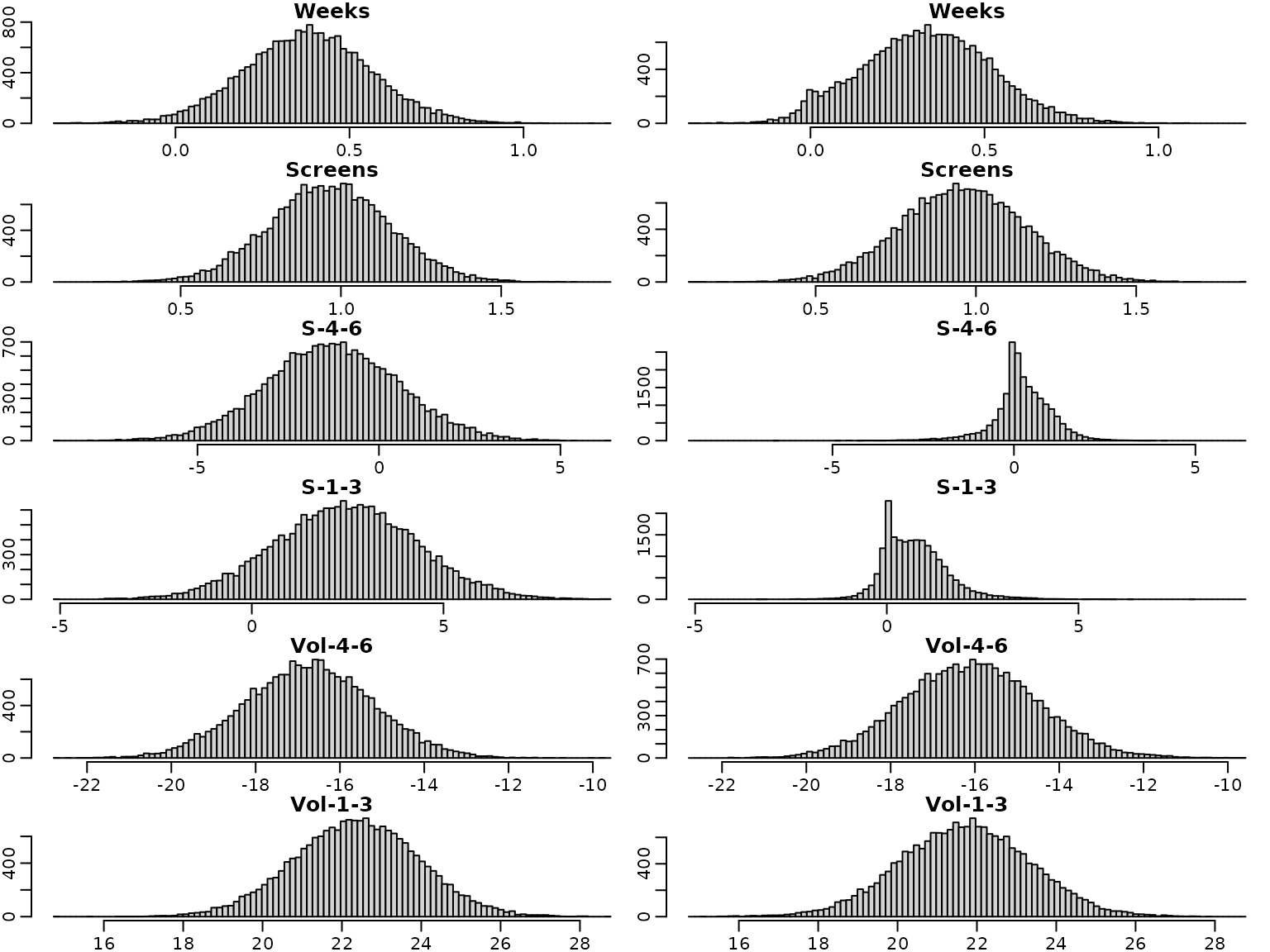
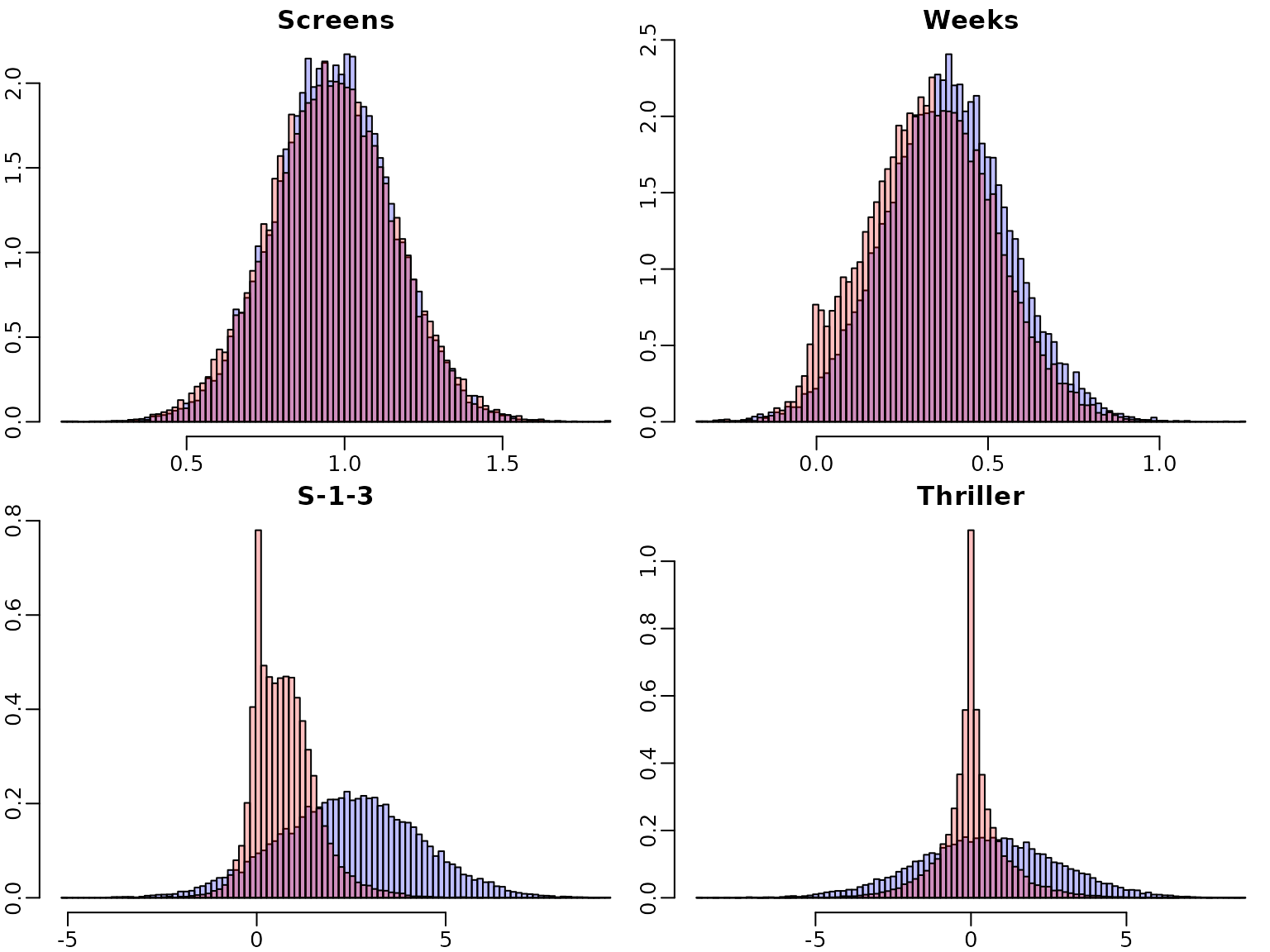
For illustration purposes, we overlay four selected marginal posteriors in order to illustrate the shrinkage effect.

selection <- c("Screens", "Weeks", "S-1-3", "Thriller")
for (i in selection) {
 breaks <- seq(min(beta.sc[,i], beta.hs[,i]), max(beta.sc[,i], beta.hs[,i]),
                length.out = 100)
 h1 <- hist(beta.sc[,i], breaks = breaks, plot = FALSE)
 h2 <- hist(beta.hs[,i], breaks = breaks, plot = FALSE)
 col <- c(rgb(0, 0, 1, 0.25), rgb(1, 0, 0, 0.25))
 plot(h1, main = i, xlab = "", ylab = "", freq = FALSE,
      ylim = c(0, max(h1$density, h2$density)), col = col[1])
 plot(h2, xlab = "", ylab = "", freq = FALSE, col = col[2], 
      add = TRUE)
}

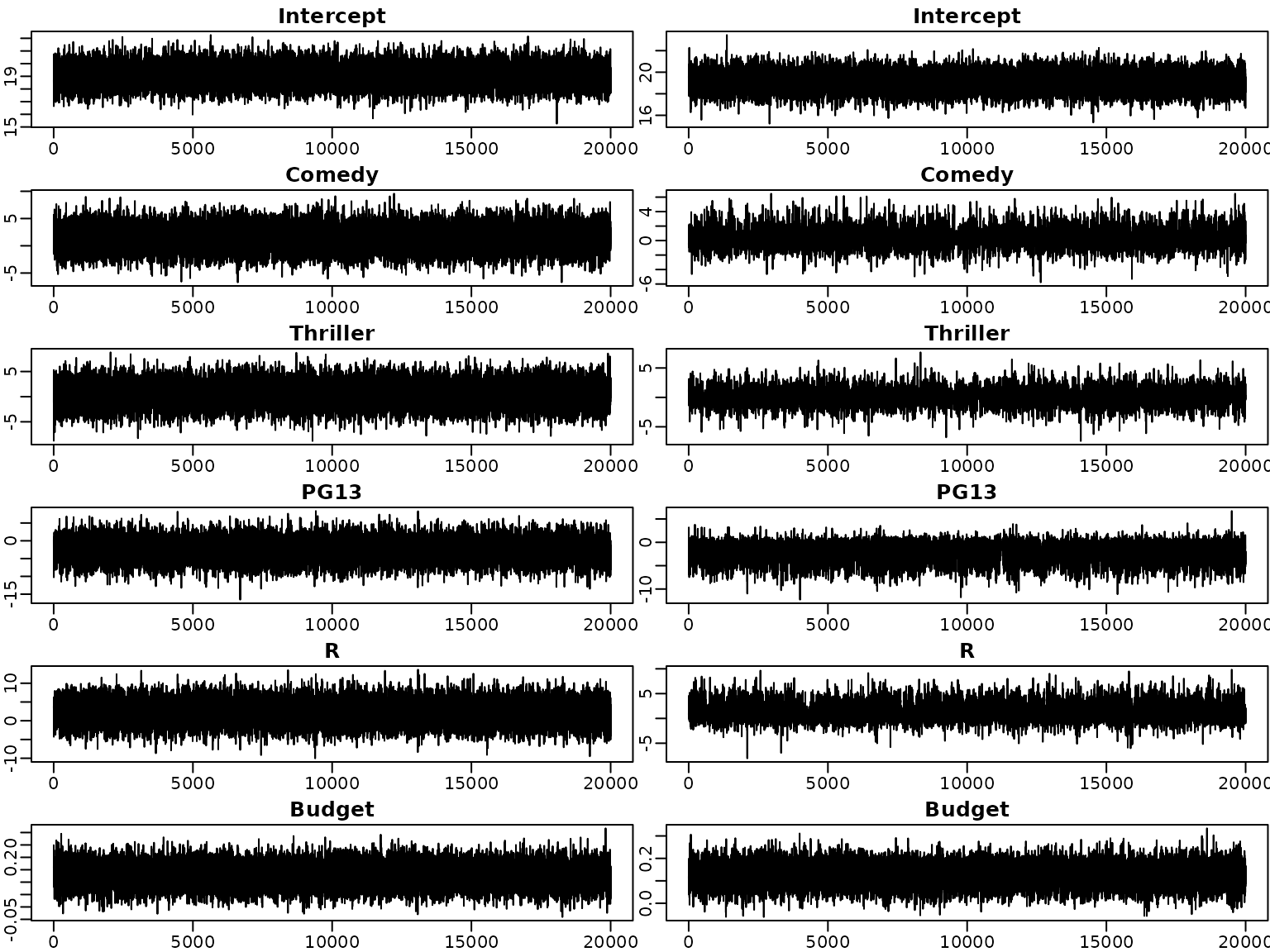
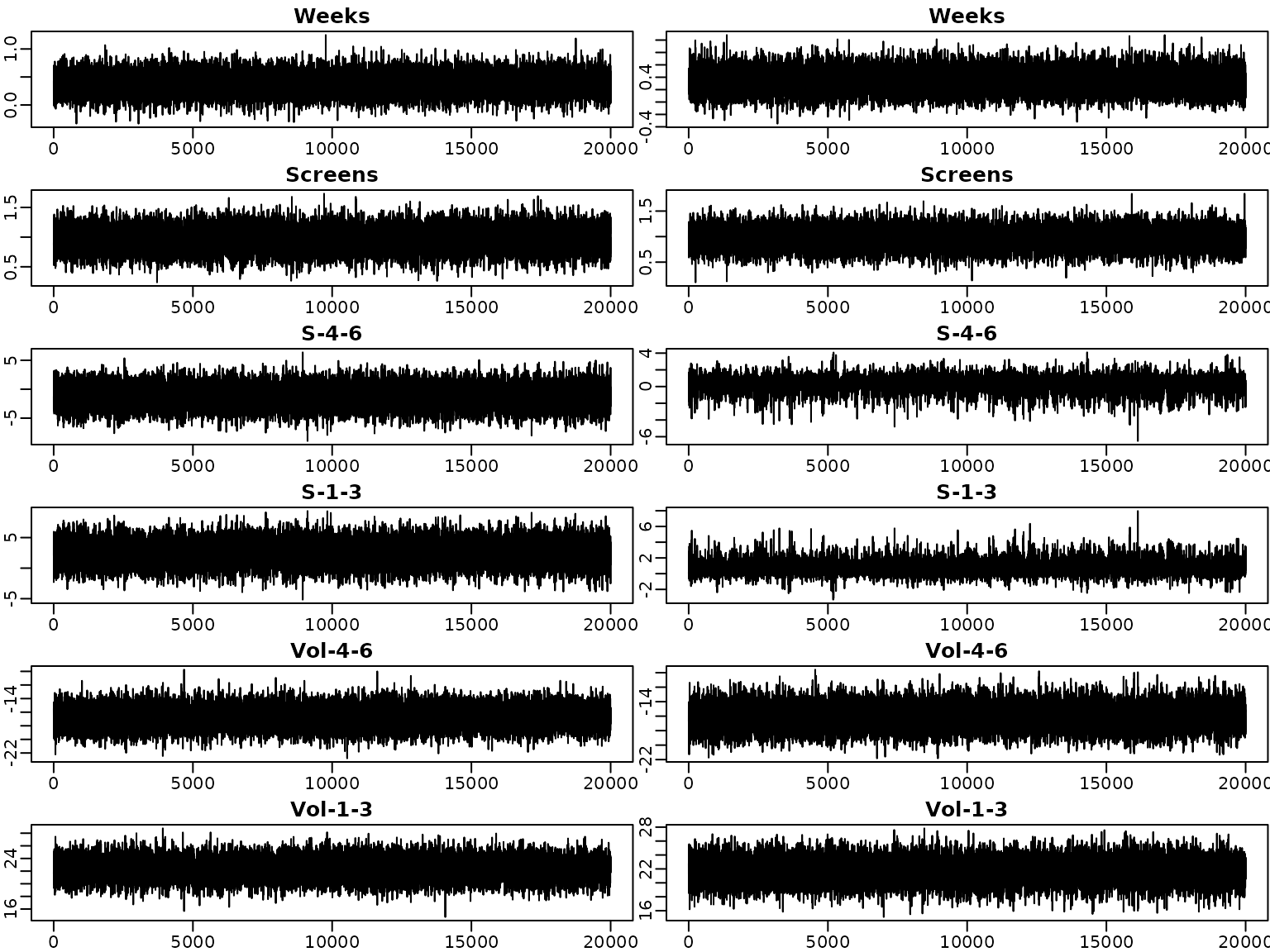
We next investigate the trace plots of the draws from the posterior. As above, the plots on the left are obtained under the semi-conjugate prior, those on the right under the horseshoe prior.

par(mfrow = c(6, 2))
for (i in seq_len(d)) {
  plot(beta.sc[,i], type = "l", xlab = "", ylab = "", main = colnames(beta.sc)[i])
  plot(beta.hs[,i], type = "l", xlab = "", ylab = "", main = colnames(beta.sc)[i])
}

To sum up, we visualize the posterior of the effects and corresponding (square root of the) shrinkage parameters. For visual inspection, we create a gap plot, where we remove the largest 5% of the local shrinkage parameter draws and mirror them around 0. That way, we can easily identify “significant” effects via clear bimodality or even a gap around zero – hence the name.

tau2.hs <- post.draws.hs$tau2s
alpha <- 0.05
truncate <- function(x, alpha) x[x <= quantile(x, 1 - alpha)] 
tau2.hs.trunc <- apply(tau2.hs, 2, truncate, alpha = alpha)
tau.hs.trunc.mirrored <- rbind(sqrt(tau2.hs.trunc), -sqrt(tau2.hs.trunc))

On the left, we see the posteriors of the regression effects posteriors, on the right, we visualize the gap plot.

We verify convergence of the sampler by doing a second run of the six block sampler in Algorithm 6.2. In the Q-Q plot of the draws of the intercept and the error variance the draws are very close to the identity line and hence we can conclude that the sampler has converged.

post.draws.hs2 <- reg_hs(y, X, M = M)

par(mfrow = c(1, 2))
qqplot(post.draws.hs$betas[, 1], post.draws.hs2$betas[, 1], 
       xlim = range(post.draws.hs$betas[, 1], post.draws.hs2$betas[, 1]),
       ylim = range(post.draws.hs$betas[, 1], post.draws.hs2$betas[, 1]),
       main = "Q-Q plot for the intercept", xlab = "", ylab = "" )
abline(a = 0, b = 1)
qqplot(post.draws.hs$sigma2s, post.draws.hs2$sigma2s,
       xlim = range(post.draws.hs$sigma2s, post.draws.hs2$sigma2s),
       ylim = range(post.draws.hs$sigma2s, post.draws.hs2$sigma2s),
       main = "Q-Q plot for the error variance", xlab = "", ylab = "")
abline(a = 0, b = 1)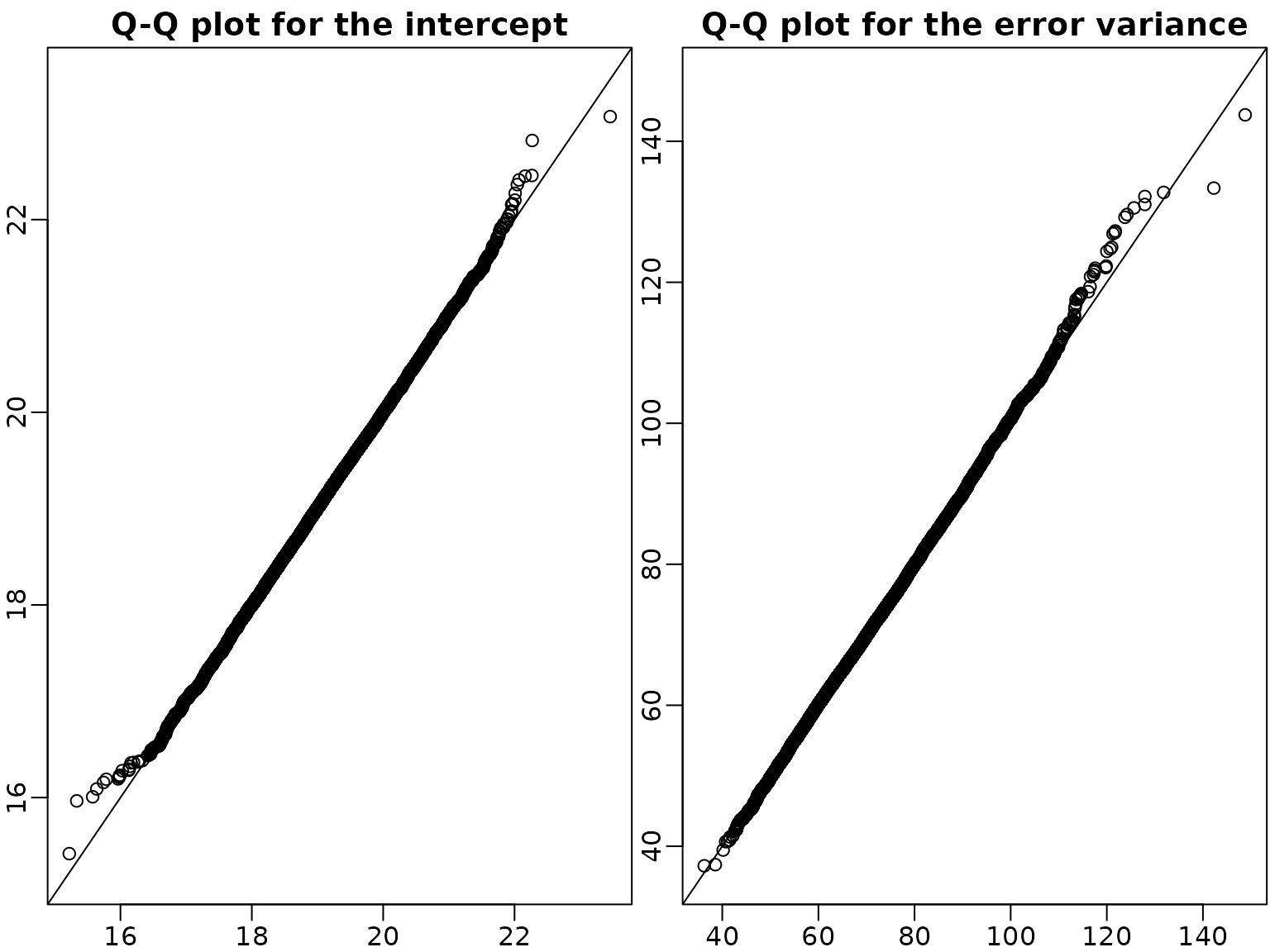

Next we predict the box office sale for different movies: a film with baseline values in all covariates (A), a film with baseline values in all covariates except genre (B) or and finally a film of genre with MPAA rating PG13 (D).

 nf=4
 X_new <- cbind(rep(1,nf), matrix(0,nrow=nf,ncol=p))
 colnames(X_new)<-colnames(X)
 
 X_new[2,"Comedy"]=1
 X_new[3:4,"Thriller"]=1
 X_new[3,"PG13"]=1
 X_new[4,"R"]=1
  
 X_new[,"Budget"]=c(10)
 
 ypred.sc=X_new%*%t(beta.sc)+rnorm(sqrt(sigma2.sc))
 pred.int.sc<- apply(ypred.sc,1, quantile, probs=c(0.025,0.5, 0.975))
 pred.mean.sc<- rowMeans(ypred.sc)
 
 ypred.hs<-X_new%*%t(beta.hs)+rnorm(sqrt(sigma2.hs))
 pred.int.hs<- apply(ypred.hs,1, quantile, probs=c(0.025,0.5, 0.975))
 pred.mean.hs<- rowMeans(ypred.hs)

We plot the predicted expectation,the median of the predictive distribution, together with vertical bars indicating the pointwise equal-tailed 95%-predictive interval


matplot(x=t(matrix(1:nf,ncol=3, nrow=nf)),y=pred.int.sc,col="blue",type = "l",pch=16,lty=1,ylim=c(8,32), xlim=c(0.5,nf+0.5), xlab="Scenarios", ylab="Predicted Open Box Office",xaxt="n")
points(x = 1:nf, y = pred.int.sc[2,], pch=19,col="blue",cex=1.2)
points(x = 1:nf, y = pred.mean.sc, pch=16,col="red")

matplot(x=t(matrix((1:nf)+0.2,ncol=3, nrow=nf)),y=pred.int.hs,col="blue",type = "l",pch=16,lty=1,add=TRUE) 

points(x = (1:nf)+0.2, y = pred.int.hs[2,], pch=19,col="blue",cex=1.2)
points(x = (1:nf)+0.2, y = pred.mean.hs, pch=16,col="red")     

axis(1,at=1:nf,labels=c("A","B","C","D"))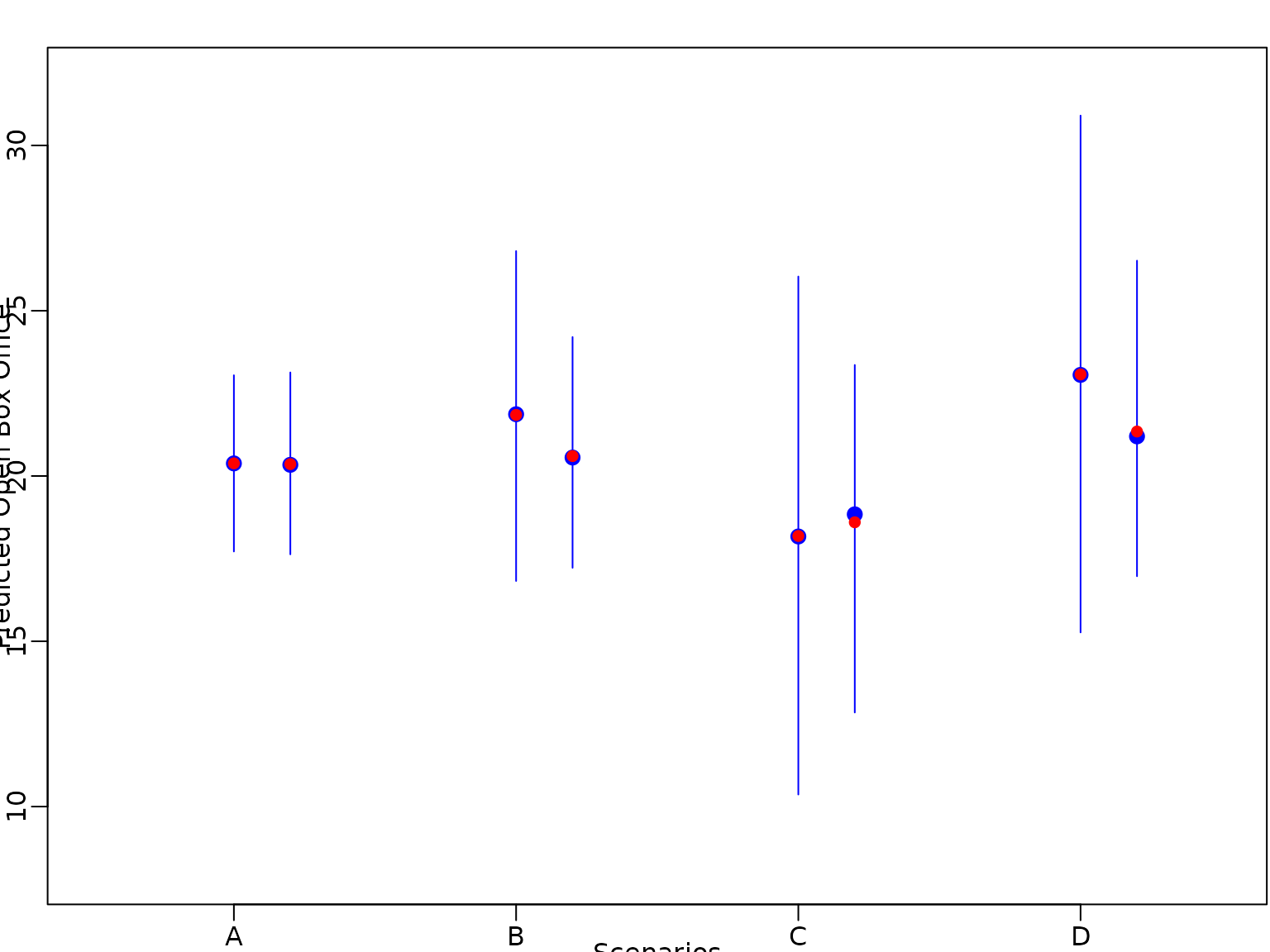

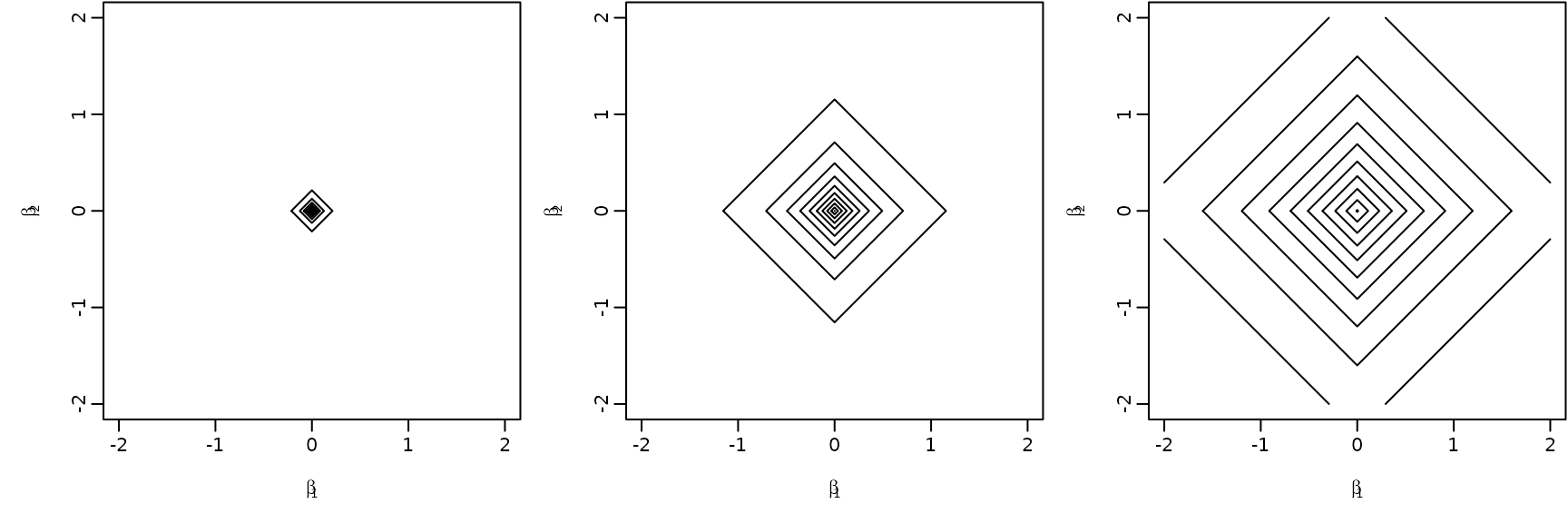
Section 6.5: Shrinkage beyond the Horseshoe Prior

Example 6.10 


beta2<- beta1 <- seq(from = -2, to = 2, by =0.01)

f <- function(x1, x2){
        exp(log(a+1)+log(a)+a*log(a) - (a+2)*log(a+abs(x1)+ abs(x2)))
}
av <- c(0.1,1,100)
par(mfrow=c(1,3))
par(mar = c(4.5, 4.5, .1, .1), 
     mgp = c(2.6, .6, 0))
for(i in 1:length(av)){
    a <- av[i]
    z <- outer(beta1, beta2, f)
    contour(beta1, beta2,z,nlevels=10, 
            xlab=expression(beta[1]),ylab=expression(beta[2]),
            drawlabels=FALSE)
}